---

車輪型倒立振子

倒立振子というのは、そのままほっておくと倒れてしまうようなものをうまくバランスをとって立ったままに保つロボットです。よくホウキや傘をひっくり返して手の上でバランスをとるように遊んだと思いますが、それをロボットにやらせようというわけです。

モータが二つ余っていたので何かできないかと考えて作り始めましたが思ったより難しく、かなり時間もかかりました。倒立振子というのは制御工学でよく扱われるテーマで、良い勉強になりました。一応制御工学は大学で学んだハズなんですけどね...

---

特徴

この倒立振子にはセンサはジャイロセンサしか搭載していません。オーソドックスな倒立振子はジャイロセンサ、ロータリーエンコーダ、電流センサの3つを搭載します。それぞれ本体の角度、モータの回転角度、モータのトルクを検出するのに必要です。これを補うために、「カルマンフィルタ」という技術でモータの角度を推定しています。またモータの電流の代わりに電圧を制御して安定化を図っています。制御の手法としては「最適制御」というのを使っています。このカルマンフィルタと最適制御を組み合わせた制御をLQGレギュレータと言うそうで、制御工学の世界では有名らしいです。まあ要するにセンサ１個だけですごいよってことです。

---

本体の構造

左は側面からの写真です。構造と言っても車輪の付いたモータに本体が乗っかっているだけです。モータが固定されたフレームの上に単4エネループ4本の電池が搭載されています。そして一番上にマイコンやジャイロセンサの載った電子回路基板がのっています。サイズは高さが120mm、幅が210mmくらいです。またタイヤの直径は100mmほどです。

---

動作

振子が倒れそうになると、倒れる方向にタイヤを回してバランスをとっていることが分かります。多少手でこづかれたりしても平気です。ゆらゆら揺れているのはモータの歯車のバックラッシュの影響が大きいと思います。他にも本体をモデル化するときの誤差なんかも影響しているのではないでしょうか。

---

---

↓ここから先はおまけの解説です↓

---

状態方程式

カルマンフィルタや最適制御を使うためには制御対象（倒立振子）を数式で表さなければなりません。これをモデル化といいます。まずは力学の方程式を導きます。ニュートンの運動方程式を使って導くこともできますが、制御対象が複雑な場合はラグランジュの運動方程式というのを使うとより簡単に式を導くことができます。

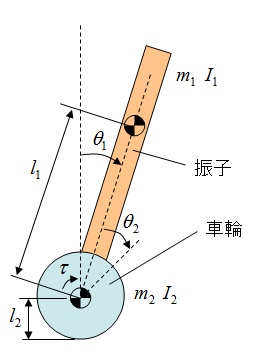
制御対象を右の図のように表します。このとき運動方程式は次のように表せます。

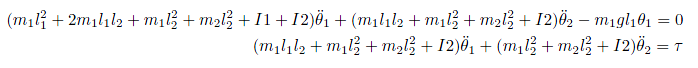
ただし各変数は次のような意味を持ちます。

• θ₁ :鉛直方向からの振子の角度
• θ₂ :振子と車輪の相対角度
• m₁ :振子の質量
• m₂ :車輪の質量
• I₁ :振子の慣性モーメント(重心まわり)
• I₂ :車輪の慣性モーメント(重心まわり)
• l₁ :モータの軸(車輪の軸)と振子の重心との距離
• l₂ :車輪の半径
• τ:モータのトルク

また、それぞれの角度および角速度は微小と考え、

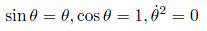
として式を計算しています。

注意しなければならないのは、この式はあくまで近似の式です。現実の世界には空気抵抗やタイヤの摩擦など色々な要因があり、振子の運動に影響を与えます。しかしこれらの要素をすべて盛り込むと式が複雑になり、また数学的に扱いにくいといった問題も出てきます。ですので程々のところで止めておきます。

さて上の式ではモータのトルクを用いています。DCモータではトルクは電流に比例しますので電流を制御できればトルクも制御できることになりますが、あいにくこのロボットは電流センサを備えておらずトルク制御は難しいです。一方、モータに入力する電圧であれば、PWMのデューティ比で直接制御することができます。そこでトルクを電圧の式に直していきます。

トルクは電流に比例し、その比例定数をK_mとおくと

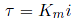
となります。また電気回路の方程式を立てると、モータへの入力電圧をv としたとき、

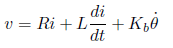
となります。ここでL=0とみなすと(ちょっと乱暴ですが)

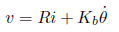
となり、i についての式に変形すると

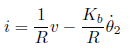
となります。これを先程の

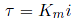
に代入すると

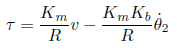
となり、トルクτと電圧v の関係が得られます。ただしK_bとK_mは実は同じ値なので(次元を計算すると同じになる)K_b=K_mとします。したがって上の式は

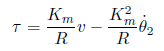
と書けます。これを上記の運動方程式の2つ目の式に代入すると、

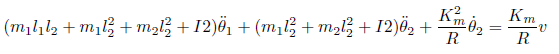
と書き直せます。これで電圧を用いた運動方程式が得られました。

これらの運動方程式を行列の形にまとめると、以下の状態方程式が得られます。出力yはジャイロセンサで測定できる振子の角速度としています。

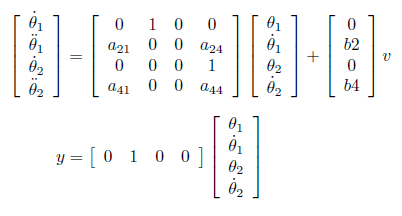
ここで、各ベクトル、行列を次のようにおけば



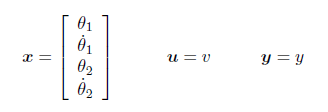
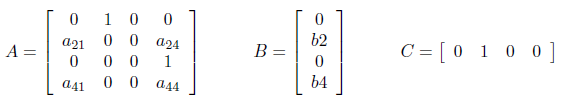
典型的な状態方程式の形として次のように書き表すことが出来ます。

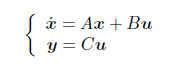
ただし、各要素は次のようになります。間違いが無いか心配(汗)

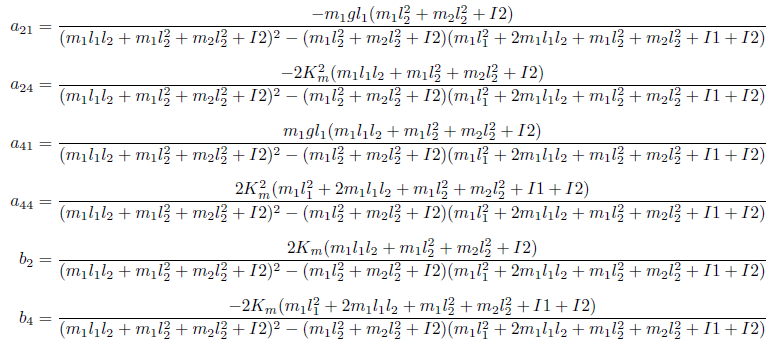
出力y はここでは振子の角速度としています。この出力をジャイロセンサで測定し、カルマンフィルタにフィードバックすることになります。

---

カルマンフィルタ

機械を制御するときには状態を直接測定するのが難しい場合がよくあります。今回製作したロボットで言えばモータにセンサを設けていないため、モータの回転角度を測定することが出来ません。このようなとき、機械の出力値から状態を推定する技術を用います。これをオブザーバといいます。その中でもよく用いられるものとしてカルマンフィルタがあります。現実の世界では、センサの測定値やモータの入力電圧にはノイズが乗ります。カルマンフィルタではこのノイズを平均ゼロのガウス分布をとるノイズであると仮定します。このノイズを踏まえた上で誤差の期待値が最も小さくなるように状態を推定する技術をカルマンフィルタと言います。

理屈的なことは難しいので（というかよく理解できていないので）簡単にカルマンフィルタの動作を説明します。下の図のようにカルマンフィルタは1時刻毎に2つの動作をします。ひとつは濾波、もうひとつは予測です。濾波とは現在の状態x^~を推定すること、予測とは未来の状態xを推定することです。濾波によって推定された現在の状態を用いて状態フィードバックを行い、制御を行います。

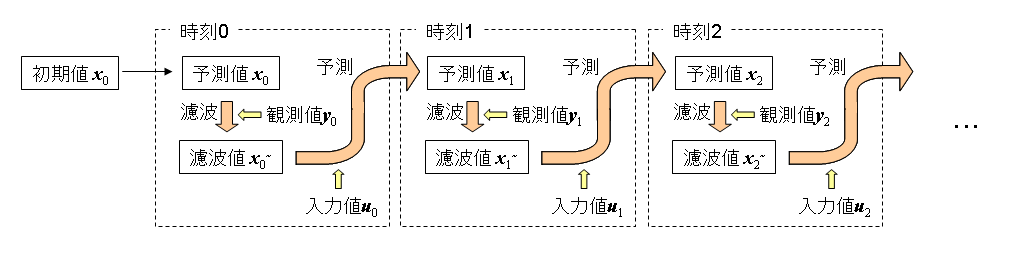
例として時刻1での手順を説明します。ひとつ前の時刻で予測した状態x₁ と現在の時刻でのセンサからの観測値y₁ を用いて濾波(現在の状態の推定)を行ない、推定値x₁^~ を計算します。次に濾波によって計算した現在の状態x₁^~ と現在の入力u₁ を用いて予測(次の時刻での状態の推定)を行ない、推定値x₂ を計算します。これをどんどん繰り返していくのがカルマンフィルタの動作です。また同時に推定誤差の共分散行列Pも同様に濾波と予測によって逐次計算していきます。時刻0の状態の初期値x₀ はスタート時の状態を想定して決めます。Pの初期値はx₀ が正確だと思うならば小さくすればよく、逆にx₀ が誤差を含んでいそうなときは大きくとれば良いので、様子を見ながらチューニングします。

具体的な計算式は次のようになります。まずは濾波です。

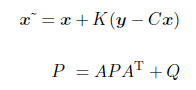
ただしK はカルマンゲインと呼ばれ

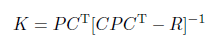
という式で計算されます。

次に予測です。予測は次のような式で計算されます。

これを繰り返し計算していくわけです。

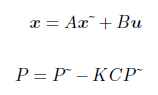
実際にカルマンフィルタを計算させるときには、設定するべき4つの値があります。システムノイズの共分散行列Q、観測ノイズの共分散行列R、そして状態の初期値x₀と誤差共分散行列の初期値P₀です。状態の初期値x₀と誤差共分散行列の初期値P₀については先ほど書きました。Rはセンサ出力をあらかじめ測定することである程度正確に求めることができます。しかしQはあらかじめ測定できないため、チューニングで決めることが多いようです。参考までに今回設定した値を書き留めておきますが、これが一番良いのかはわかりません...

---

最適制御

最適制御てすごい名前ですよね。私は初めて聞いたとき、これを使えば最高、これ以上無いみたいな印象を受けました。だって「最適」ですよ。けど中身は、ある条件をできるだけ満たすように状態フィードバックをしようというだけです。そしてその条件とは「状態や入力の絶対値ができるだけ小さくなるように」というものです。状態や入力の絶対値が小さくなれば安定だろってことだと思います。状態とはここでは本体の角度やタイヤの回転角度にあたります。また入力はモータの電圧にあたります。この条件を数式で解くにはリカッチ方程式というのを解けばよいそうです。

これがリカッチ方程式です。

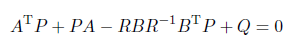
この方程式の解Pを用いて、最適フィードバックゲインKは

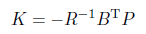
と計算されます。私はMatlabの"lqr"という関数を使ってしまいましたが...
QとRというのは重み行列でこれらの値を変化させることでどの状態を、あるいはどの入力をより小さくしたいか調節することができます。Qの4つの対角の値がそれぞれ4つの状態に対応し、Rは入力電圧に対応します。大きい値を設定するほど、その値に対応する状態あるいは入力を相対的により小さくするように出来ます。これも最良か分かりませんが設定したパラメータを参考までに書き留めておきます。

---

コントロールボード

ロボット制御用にマイコン、モータドライバ、RS232インターフェースなどをまとめた汎用コントロールボードを製作しました。別のページ(←まだ書き中)にまとめる予定です。

---

作品紹介に戻る